Predict for Winning or Losing
Section Introduction
In the first regression analysis, we have known that there are some factors significantly contributing to the number of winnings, especially some factors about three-pointer. In this section, we will continue explore the relationships between factors of all aspects and the scores made in every game, by using data from every game in the last 20 years in NBA and using logistic regression to analyze what factors might affect the game’s score to try to find out what New York Knicks needs to improve for achieving higher score.
knitr::opts_chunk$set(
fig.width = 6,
fig.asp = .6,
out.width = "90%"
)
theme_set(theme_minimal() + theme(legend.position = "bottom"))
options(
ggplot2.continuous.colour = "viridis",
ggplot2.continuous.fill = "viridis"
)
scale_colour_discrete = scale_colour_viridis_d
scale_fill_discrete = scale_fill_viridis_dData
box_score_all = read_csv("./data2/box_score_all.csv")The box_score_all dataset contains 47830 games’ data from season 2012-2013 to season 2020-2021, which includes 30 variables. We are going to use some of them in the following exploratory data analysis.
Descriptive Statistics
We should delete some variables which are not applicable for regression analysis, like season_year, team_id and some rank variables.Then select the reasonable variables to analyze to create a data set called “regre_df”
These are some reasonable variables that should be added into the regression model:
- wl: Win/Loss
- min: minutes
- pts: Points
- fgm: Field Goals Made
- fga: Field Goals Attempted
- fg_pct: Field Goal Percentage
- fg3m: 3 Point Field Goals Made
- fg3a: 3 Point Field Goals Attempted
- fg3_pct: 3 Point Field Goals Percentage
- ftm: Free Throws Made
- fta: Free Throws Attempted
- ft_pct: Free Throw Percentage
- oreb: Offensive Rebounds
- dreb: Defensive Rebounds
- reb: Rebounds
- ast: Assists
- stl: STL
- blk: Blocks
- blka: Blocks Attempted
- tov: Turnovers
- pf: Personal Fouls
- pfd: Personal Fouls Drawn
- plus_minus: Plus-Minus
In order to build logistic regression model, we will replace win/loss with 1/0. Then draw boxplots of every variable to compare the characteristics of winning and losing teams.
regre_df =
box_score_all %>%
select(-c(1:7)) %>%
select(-ends_with("rank")) %>%
mutate(wl = recode(wl, "W" = 1, "L" = 0),
wl = as.factor(wl)) Exploratory Analysis
In this part, we explore each game in the past 20 years, try to find some important variables that might affect the result of the game. By this process, we also can get some insight on choosing potential parameters for model building.
Difference average scores
Firstly, we take a look on the scores difference between the winning team and losing team in the past 20 years.
We can see that if a team wants to win the game, the score they needs to achieve become much higher compared to the past years. The average score for the winning team has comes up and down from 2001-2015 seasons, however, after entering the small ball revolution, the average score for winning keep increase and never fall down since 2015-16 season.
So, it is obviously that if a team wants to win a game, they need to find a new techniques to earn more score. Next we will explore some factors we think might play a big rule on the result of the game.
lose_game=
box_score_all %>%
filter(wl == "L")
box_score_all %>%
filter(wl == "W") %>%
ggplot(aes(x = pts, y = season_year)) +
geom_density_ridges(scale = .8, alpha = .5, fill = "blue",
quantile_lines = T, quantile_fun = mean) +
geom_density_ridges(data = lose_game, aes(x = pts, y = season_year),
scale = .8, alpha = .5, fill = "salmon",
quantile_lines = T, quantile_fun = mean) +
scale_fill_manual(name = "Team", values = cols) +
xlim(65, 140) +
labs(x = "Scores",
y = "Season Year",
title = "Score Distribution Win and Lose game") 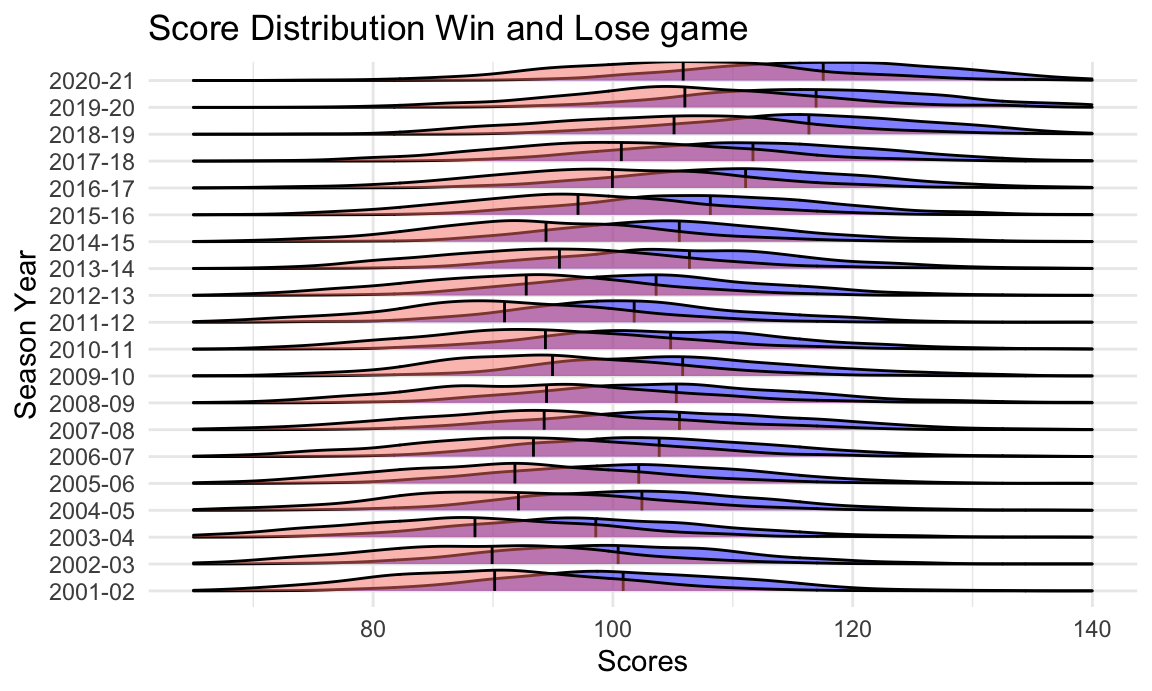
Variables can affect the result of game
As a team needs to gain more score for winning the game, to analyze the factors of game result, we first look at some variables that directly have influence on score. We put both the plot of percentage and attempted together, so we can observe NBA’s trend of scoring strategy in these 20 years.
First, we can see that although the field goal attempted and percentage didn’t seems to have much change through these 20 years,the winning team have much stronger field goal percentage compare the team who lose. Also, we can see that the losing team have a slightly more field goal attempted than the winning team.
Secondly, we can see that the 3 point field goals’ percentage didn’t change much in these two decades.However, there is a really significant increase on the 3 point field goals attempted. After the small ball era at 2015, the 3 point field goals attempted grow up remarkably, also we can see the same pattern as field goal attempted, the losing team have a higher 3 point field goals attempted.
Third, we can see that free throw attempted and percentage didn’t have much change through these 20 years. And the winning teams have higher attempted and percentage.
By inspect these variables, we can conclude that on the basketball field, there are almost like a three points field goals fight after 2015, everyone throw as much as 3 points play as they can. The most notable difference of attempted between winning team and losing team happened on the free throw attempted, this means that even that the free throw only contribute one point in the score, it still is an indicator of the game result. And the most outstanding difference of percentage between winning team and losing team happened on the field goal percentage, this suggest that to improve field goal percentage is one of the most critical thing a team should consider if they want to win the game.
So since 3 points field attempted become trend in every game, we look up three of the most higher 3 points field attempted outliers on the plot. We find out it all made by Houston Rockets, so we took a look deeply, we find out in the top ten of the highest 3 points field in these 20 years, Houston Rockets occupy 8 and the other 2 is Atlanta Hawks.
Field Goal
plot_ly( box_score_all, x = ~ season_year, y = ~ fga , color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Field Goal Attempted"))plot_ly( box_score_all, x = ~ season_year, y = ~ fg_pct, color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Field Goal Percentage"))3 Point Field Goals
plot_ly(box_score_all, x = ~ season_year, y = ~ fg3a, color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "3 Point Field Goals Attempted"))plot_ly(box_score_all, x = ~ season_year, y = ~ fg3_pct, color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "3 Point Field Goals Percentage"))Free Throw
plot_ly(box_score_all, x = ~ season_year, y = ~ fta, color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Free Throw Attempted"))plot_ly(box_score_all, x = ~ season_year, y = ~ ft_pct, color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Free Throw Percent"))New York Knicks 3 Point Field Goals
Since, in the previous part, we found out that highest 3 points field in these 20 years, Houston Rockets occupy 8 of it and the other 2 is Atlanta Hawks. It seems like there are some team really superior in 3 points. So we take a look of Knicks’s 3 Point Field Goals and 3 Point Field Goals Attempted, we found out that even after the small ball era, Knicks’s average of 3 Point Field Goals and Attempted didn’t have much increase.
nyk=
box_score_all %>%
filter(team_abbreviation =="NYK")3 Point Field Goals Attempted
plot_ly(nyk, x = ~ season_year, y = ~ fg3a, color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "3 Point Field Goals Attempted"))3 Point Field Goals Percentage
plot_ly(nyk, x = ~ season_year, y = ~ fg3_pct, color = ~ wl, type = "box") %>%
layout(boxmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "3 Point Field Goals Percentage"))Offensive Level Parameters
Next, we are going to explore the influence of some offensive strategies on the basketball field, to see what kind of techniques might play a big role on the result of the game.
The average offensive rebounds is slightly higher in the losing team. And on the average assists per game, winning team is significantly higher than losing team.
Average offensive rebounds are higher in the losing team seems like a same pattern as the attempted also higher in the losing team. We can hypothesize that when a team starting to lose, they will take more aggressive strategies compared to the team that keep leading .
Average assists per games is significantly higher in the winning team, this might result from the assists is defined as scoring successfully, and more scoring means more possible to win.
offensive_df =
box_score_all %>%
select(season_year,wl, oreb, ast)Average offensive rebounds per game
offensive_df %>%
group_by(season_year, wl) %>%
summarise(oreb= mean(oreb)) %>%
plot_ly(x = ~ season_year, y = ~ oreb, type = "bar",
color = ~wl, colors = "viridis") %>%
layout(barmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Average offensive rebounds of each game"))Aaverage assists per games
offensive_df %>%
group_by(season_year, wl) %>%
summarise(ast= mean(ast)) %>%
plot_ly(x = ~ season_year, y = ~ ast, type = "bar",
color = ~wl, colors = "viridis") %>%
layout(barmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Aaverage assists of each game"))Defensive level Parameters
In this part, we are going to explore the influence of some defensive level strategies on the basketball field, to see what kind of defensive techniques might play a role on the result of the game.
Steals, Blocks, Defensive rebounds of each game is significantly higher in the winning team, Personal foul and Turnovers of each game are slightly higher in the losing team.
defensive_df =
box_score_all %>%
select(season_year,wl,stl,blk,dreb,tov, pf)Steals of each game
box_score_all %>%
group_by(season_year, wl) %>%
summarise(stl= mean(stl)) %>%
plot_ly(x = ~ season_year, y = ~ stl, type = "bar",
color = ~wl, colors = "viridis") %>%
layout(barmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Aaverage steals of each game"))Blocks of each game
box_score_all %>%
group_by(season_year, wl) %>%
summarise(blk= mean(blk)) %>%
plot_ly(x = ~ season_year, y = ~ blk, type = "bar",
color = ~wl, colors = "viridis") %>%
layout(barmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Aaverage blocks of each game"))Defensive rebounds of each game
box_score_all %>%
group_by(season_year, wl) %>%
summarise(dreb= mean(dreb)) %>%
plot_ly(x = ~ season_year, y = ~ dreb, type = "bar",
color = ~wl, colors = "viridis") %>%
layout(barmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Aaverage defensive rebounds of each game"))Turnovers of each game
box_score_all %>%
group_by(season_year, wl) %>%
summarise(tov= mean(tov)) %>%
plot_ly(x = ~ season_year, y = ~ tov, type = "bar",
color = ~wl, colors = "viridis") %>%
layout(barmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Aaverage turnovers of each game"))Personal foul of each game
box_score_all %>%
group_by(season_year, wl) %>%
summarise(pf= mean(pf)) %>%
plot_ly(x = ~ season_year, y = ~ pf, type = "bar",
color = ~wl, colors = "viridis") %>%
layout(barmode = "group",
xaxis = list(title = 'Season Year'),
yaxis = list(title = "Aaverage personal foul of each game"))Corralation Map
Further, we draw a correlation map to exam correlation of each variables, this process can help us select variables for building our logistic model.
regre_df =
regre_df %>%
mutate(
min = as.numeric(min),
fgm = as.numeric(fgm),
fga = as.numeric(fga),
fg_pct = as.numeric(fg_pct),
fg3m = as.numeric(fg3m),
fg3a = as.numeric(fg3a),
fg3_pct = as.numeric(fg3_pct),
ftm = as.numeric(ftm),
fta = as.numeric(fta),
ft_pct = as.numeric(ft_pct),
oreb = as.numeric(oreb),
dreb = as.numeric(dreb),
reb = as.numeric(reb),
ast = as.numeric(ast),
tov = as.numeric(tov),
stl = as.numeric(stl),
blk = as.numeric(blk),
blka = as.numeric(blka),
pf = as.numeric(pf),
pfd = as.numeric(pfd),
pts = as.numeric(pts),
plus_minus = as.numeric(plus_minus)
)
corr <- cor(regre_df[-1])
corrplot(corr, method = "square", order = "FPC")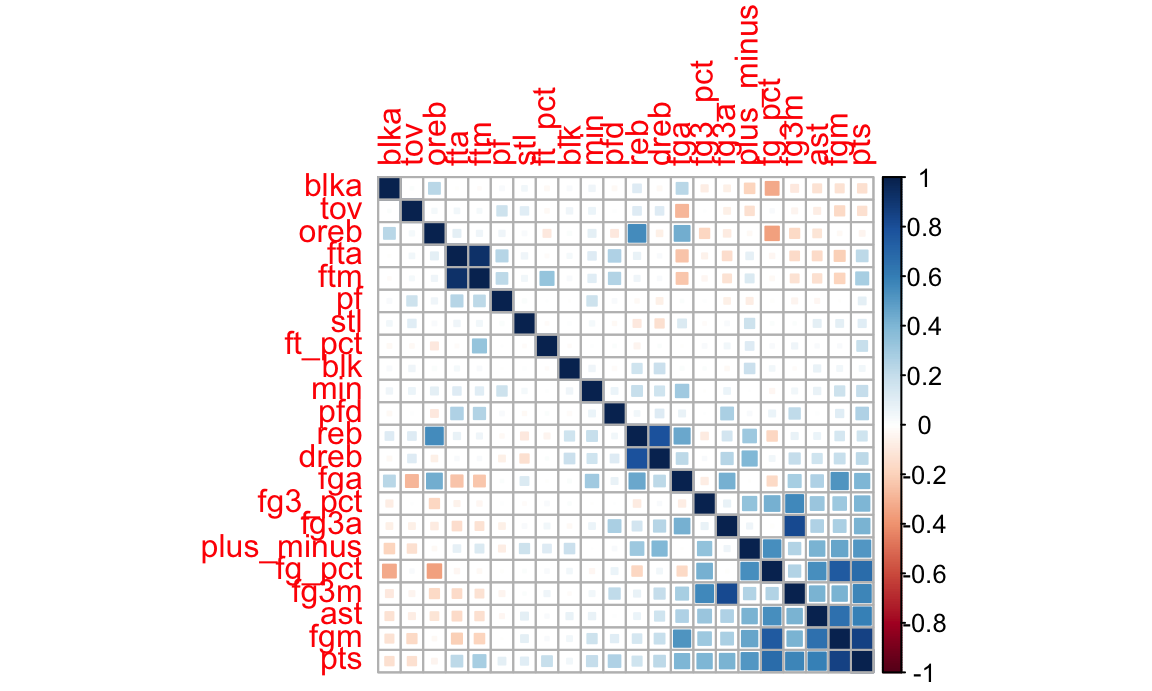
Based on this plot, we can see that there are strong correlation between some variables, like ftm and fta, dreb and reb. We will select one variable from a pair of variables that have strong correlation (which is more than 0.5). And we can select variables which have no strong correlation with others.
Logistic Regression
Separate data as 80% training data and 20% testing data for prediction.
set.seed(22)
train.index <- sample(x=1:nrow( regre_df), size=ceiling(0.9*nrow(regre_df)))
train = regre_df[train.index, ]
test =regre_df[-train.index, ]Modelling
Based on the correlation plot above, we choose the variables we are interested and build logistic regression model using stepwise regression.
lg_regre<-glm(wl~fg_pct+fg3_pct+ft_pct+oreb+dreb+ast+stl+blk+tov+pf,data =train, family = "binomial",control = list(maxit=1000))
logit.step = step(lg_regre,direction="both")lg_regre %>% broom::tidy() %>% knitr::kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -25.1502742 | 0.2823800 | -89.06535 | 0 |
| fg_pct | 30.3007189 | 0.3946944 | 76.77008 | 0 |
| fg3_pct | 4.3004764 | 0.1322090 | 32.52786 | 0 |
| ft_pct | 3.6269519 | 0.1339344 | 27.08006 | 0 |
| oreb | 0.1691057 | 0.0038275 | 44.18163 | 0 |
| dreb | 0.2375430 | 0.0031526 | 75.34752 | 0 |
| ast | -0.0408460 | 0.0032164 | -12.69913 | 0 |
| stl | 0.2632653 | 0.0051024 | 51.59663 | 0 |
| blk | 0.1203968 | 0.0053404 | 22.54450 | 0 |
| tov | -0.1776777 | 0.0037780 | -47.03018 | 0 |
| pf | -0.0671351 | 0.0030500 | -22.01118 | 0 |
Interpretation of model coefficients
For logistic regression, we can explain variables from the perspective of odds.
All variables selected are significant in this logistic regression model.
For each additional 1 of proportion of field goals attempted, the odds of win over loss will become \(e^{30.300719}\) times.
For each additional 1 of proportion three points shooting, the odds of win over loss will become \(e^{4.300476}\) times.
For each additional 1 of proportion of free throw, the odds of win over loss will become \(e^{3.626952}\)times.
For each additional 1 of offensive rebounds per game, the odds of win over loss will become \(e^{0.169106}\) times.
For each additional 1 of defensive rebounds per games, the odds of win over loss will become \(e^{0.237543}\)times.
For each additional 1 of steals per game, the odds of win over loss will become \(e^{0.263265}\) times.
For each additional 1 of assists per game, the odds of win over loss will become \(e^{-0.040846}\) times.
For each additional 1 of blocks per game, the odds of win over loss will become \(e^{0.120397}\) times.
For each additional 1 of turnovers per game, the odds of win over loss will become \(e^{-0.177678}\)times.
For each additional 1 of personal foul per game, the odds of win over loss will become \(e^{-0.067135}\) times.
Calculate prediction accuracy.
probabilities <- lg_regre %>% predict(test, type = "response")
head(probabilities)
contrasts(test$wl)
predicted.classes <- ifelse(probabilities > 0.5, "1", "0")
head(predicted.classes)mean(predicted.classes == test$wl)## [1] 0.8053523Using the logistic model of all variables we selected, the prediction accuracy is 0.8053523.
Conclusion
Our final model for predicting game result is showing below.
\[Y_i=-25.150274 + 30.300719 (fg_pct)+4.300476(fg3_pct)+3.626952(ft_pct)+0.169106(oreb)+\\ 0.237543(dreb)-0.040846(ast)+0.263265(stl)+0.120397(blk)-0.177678(tov)-0.067135(pf)\] We have built both linear and logistic regression based on the NBA data. The adjusted R square for the linear regression model is 0.6916, which can explain the game score in a large extent. And the prediction of the logistic regression model is 0.8053523, which can help us to predict the result of the game correctly. There are some variables that can positively attribute to the winning of a game in both two models, like proportion of field goals attempted, proportion three points shooting and proportion of free throw, which can instruct the Knicks to pay more attention on these aspects in daily training. There is variable that can negatively attribute to the winning of a game in both two models, turnovers, which can instruct the Knicks to avoid this action in games.